 |
BALLON de BAUDRUCHE(1) |
BALLON de BAUDRUCHE
photo : Alain F6AGV
Il est facile de se procurer un ballon de baudruche, un peu plus difficilement de l'hélium. Mais la commercialisation de bouteilles de faible capacité hélium pour les ballons de baudruches permet d'envisager des expériences à domicile ou dans les écoles. Sur cette photo, le ballon est parfaitement immobile en suspension dans l'air dans une pièce sans vent. Il soulève une charge utile constituée par une feuille de papier A4 à l'origine et une ficelle. L'enveloppe jaune contient l'hélium mais celle ci étant poreuse, on pourra observer au bout d'un certain temps une chute soudaine du ballon. A ce moment, il suffit de couper la feuille de papier pour lâcher du lest et le ballon monte jusqu'au plafond pendant un bon moment et ainsi de suite. Avec un peu d'effort et d'adresse on arrive à immobiliser le ballon entre le sol et le plafond, avec un léger courant d'air on découvre le vol des ballons à gaz en modèle réduit.
Bilan des masses :
L'enveloppe baudruche : 2 grammes, ficelle : 1 gramme, nacelle en papier : 2 grammes et la masse de l'hélium dans le ballon ( inconnue ).
Pour trouver quelle est la masse de l'hélium, il faut connaître le volume interne du ballon.
Le diamètre fait 0,21 mètre, mais le ballon n'est pas sphérique, il y aura une approximation dans les calculs qui vont suivre. Une méthode de mesure du volume serait possible pour davantage de précision.
Le rayon est égal au diamètre divisé par 2 : r = 0,105 m
Le volume est 4/3 . Pi . r 3 = 4/3 . 3,141632 . ( 0,105 ) 3 = 4,1887 . ( 0,105 ) 3 = 0, 0048489 m3
Pour tenir compte de la forme réelle du ballon, un coefficient est trouvé : k = 1,1 ( méthode empirique ). Vb = 0, 0048489 . 1,1 = 0,00533 m3
La masse de l'hélium est connu à partir de la masse volumique de l'hélium : la masse de l'unité de volume c'est 0,163 kg/ m3 .
Cette valeur n'est pas constante car elle va dépendre de la température et de la pression au moment des essais.
Voir la
feuille de calcul Excel : ![]()
La masse de l'hélium est : MHe = RhoHe . Vb = 0,163 . 0,00533 = 0, 0008688 kg poids de l'hélium = PHe = 0,0008688 . 9,81 = 0,0085228 N
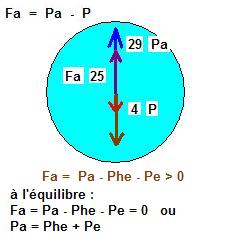
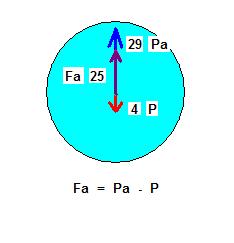
Poussée d' Archimède : Pa = Rhoair . Vb . g = 1,18 . 0,00533 . 9,81 = 0, 0617 N
La force ascensionnelle Fa est Fa = Pa - PHe = 0,0617 - 0,0085228 = 0,05317 N
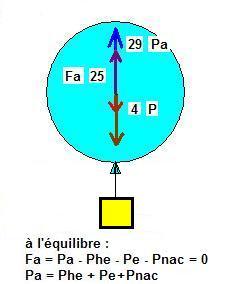
La force ascensionnelle libre Fal est Fal = Fa - Psans HE = 0,05317 - ( 0,002 + 0,001 + 0,002 ) .9,81 = 0,00412 N
Le ballon décolle et sa vitesse atteint la limite de v = 0,6067 m/s au bout de quelques secondes seulement.
Maintenant la Fal devient nulle, le ballon est immobile en suspension entre le plafond et le sol. .
Quel élément à changer dans la formule de la Fal ?
R : Les masses sont restées les même sauf la masse de l'hélium en raison des fuites avec l'enveloppe poreuse. Le volume d'hélium a diminué? mais de combien ?
Fa = Pa - PHe = Rhoair . Vb . g - RhoHe . Vb . g = Vb . g ( Rhoair - RhoHe ) = Vb . 9,81 . ( 1,18 - 0,163 ) = 9,977 . Vb
La Fal est nulle : Fal = 0 = Fa - Psans He donc Fa = Psans He = 9,977 . Vb
Le volume est devenu : Vb = ( 0,002 + 0,001 + 0,002 ) . 9,81 / 9,977 = 0,004916 m3 soit moins 0,0004137 m3
Le volume a bien diminué légèrement mais suffisamment pour faire descendre le ballon. Si le dégonflage continue cela va provoquer la chute du ballon car la Fal sera négative.
Le volume a encore diminué de 0,0005 m3 . Quel est le poids du lest à retirer pour revenir à l'équilibre et au ballon immobile ?
R : Le nouveau volume est Vb = 0,004916 - 0,0005 = 0,004416 m3
Vb = ( 0,002 + 0,001 + x ) . 9,81 / 9,977 = 0,004416 ( 0,003 + x ) . 9,81 = 0,044058
0,003 + x = 0,00449 x = 0,00149 kg ou 1,49 g
Reste à tracer une grille sur la feuille de papier sachant que la surface fait 0,21 x 0,297 m = 0,06237 m2 pour une masse de 2g soit 32,066 g / m2
photo : Alain F6AGV
Autre exemple de calculs :
Un ballon de 71 cm de circonférence est gonflé à 0°C avec de l'hélium. L'enveloppe fait 2 grammes, la ficelle fait 1 gramme et la nacelle ( feuille de papier ) fait 2 grammes.
Calculez la poussée d'Archimède Pa. Faire le bilan des masses, cherchez PsHe et calculez la force ascensionnelle libre.
On donne la masse volumique de l'air à 0°C est 1,294 kg/m3 , la masse volumique de l'hélium à 0°C est 0,178 kg/m3 .
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
R : La circonférence est c = Pi . D = 0,71 m ---> D = c / Pi = 0,71 / 3,1416 = 0,226 m le rayon est r = 0,113 m
Le volume est Vb = 4/3 . Pi . ( r )3 = 4,1887 . ( 0,113 )3 = 0,006044 m3
Rhoair = 1,294 kg/m3 Rhoair = masse / volume La poussée d'Archimède Pa est = Rhoair . Vb . g = 1,294 . 0,006044 . 9,81
Pa = 0,07672 N
La masse de l'hélium est MHe = RhoHe . Vb = 0,178 . 0,006044 = 0,0010758 kg PHe = MHe . g = 0,0010758 . 9,81 = 0,010554 N
Le bilan des masses est le suivant : ( Menv + Macc + Mnac )
PsHe = ( Menv + Macc + Mnac ) . g = ( 0,002 + 0,001 + 0,002 ) . 9,81 = 0,04905 N
La force ascensionnelle libre est Fal = Pa - Ptotal ou Fal = Fa - PsHe ou Fal = Pa - ( PHe + PsHe )
Fal = 0,07672 - ( 0,010554 + 0,04905 ) = 0,017116 N et Fa = Pa - PHe = 0,07672 - 0,010554 = 0,066166 N
Si on veut parler en grammes au lieu d'utiliser les newtons :
Pa ---> 7,82 g MHe ---> 1,0758 g PsHe ---> 5 g Fa ---> 6,7447 g Fal --> 1,74475 g
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Autre problème : Le ballon précédent se dégonfle ( poreux ) et il est en équilibre. Calculez le volume d'hélium dans ce cas ?
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
R : Fal = 0 d'où Pa = Ptotal = Phe + PsHe
1,294 . Vb = 0,178 . Vb + 0,005 ---> Vb = 0,005 / ( 1,294 + 0,178 ) = 0,00448 m3
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Suite : combien faut-il lâcher de lest pour retrouver une Fal de 1,745 g ?
R : Fal = Rhoair . Vb - ( RhoHe . Vb + PsHe ) on a simplifié par g
0,001745 = 1,294 . 0,00448 - ( 0,178 . 0,00448 + x ) ---> d'où PsHe = 0,0032547 kg = Pnac + Penv + Pacc
Pnac = 0,0032547 - Penv - Pacc = 0,0032547 - 0,002 - 0,001 = 0,0002547 kg
La masse de la nacelle passe de 2 g à 0,2547 g le LEST est égal à la masse perdue soit 1,746 g
On remarque que la force ascensionnelle libre est égale au LEST.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Suite : Avec le même ballon : Vb = 0,00448 m3 et la masse sauf hélium étant de 5 g, on a lâché 1 g de LEST. Calculez la Fal avant et après le lancé du LEST.
R : Fal = Pa - Ptotal = 1,294 . Vb - ( 0,178 . Vb + 0,005 ) = 1,294 . 0,00448 - ( 0,178 . 0,00448 + 0,005 ) = 0
Fal = 1,294 . 0,00448 - ( 0,178 . 0,00448 + 0,004 ) = 0,000999 # 0,001 kg ou 1 g
La Fal récupérée est égale au lest lancé.
 |
 |
 |
ballon au départ avec nacelle photographique, voir sous la nacelle. Photo : Alain F6AGV
documentation,
bibliographie, ouvrages, livres et articles utilisés pour établir les pages
: ![]()