 |
BALLON A GAZ (2) |
BALLON HÉLIUM

photo : internet
Exemple de calculs pour un vol de ballon : la question qui se pose est la suivante. Compte tenu, de la masse de la nacelle, de l'enveloppe et des constituants de la chaîne de vol, quel volume d'hélium faut-il utiliser ?
Choix : on se fixe une vitesse de montée limite de 5 m/s. On choisit une enveloppe latex de 1200 grammes.
Bilan des masses :
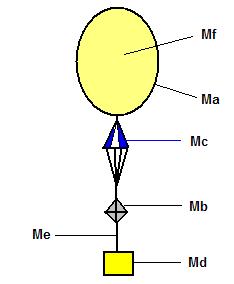 |
Ce dessin représente une chaîne de
vol classique.
Le centre de gravité de cette chaîne est quelque part sur l'axe de la chaîne de vol suivant la répartition des masses. Au départ d'un ballon, la chaîne s'incline car l'enveloppe a plus de prise au vent que la nacelle et les autres éléments, mais ensuite une fois la vitesse limite atteinte, la chaîne est verticale. On peut observer un léger balancement et une rotation de l'ensemble amplifiée par l'élasticité de la ficelle. |
exemple de calcul :
MA= masse de l' enveloppe = 1,2 kg ( Menv )
MB= masse du réflecteur radar = 0,12 kg ( Mrefl )
MC= masse du parachute = 0,26 kg ( Mpara )
MD= masse de la nacelle = 2,5 kg ( Mnac )
ME= masse des accessoires = 0 kg ( Macc )
MF= masse de l' hélium = ?????? ( Mhe ) à déterminer par le calcul ainsi que le volume d'hélium Vb.
Masse de la charge ( sans l' hélium ) : MA + MB + MC + MD + ME = 4,08 kg ( la valeur à ne pas dépasser est 4 kg ).
Poids de la charge ( sans l'hélium ) : Pb = 4,08 x 9,81 = 40 N .
1.Poussée d'Archimède : Pa = qair . Vb . g c'est à dire masse volumique de l'air x volume déplacé x 9,81 ( à une altitude donnée ).
2.Ballon hélium sans charge et sans enveloppe ( théorique ) : Fa = ( Pa - Phe ) avec Pa > Phe Fa est positif. Phe = qhe. Vb . g
C'est la valeur maximale possible pour un volume donné d'hélium.
3.Ballon complet avec charge : Fal = Pa - Ptotal > 0 avec Fal < Fa
Fal c'est la Force ascensionnelle libre ou Fa réelle à un moment donné.
Fal = Pa - ( Penv + Phe + Prefl + Ppara + Pnac ) ou Fal = Pa - Penv - Phe - Prefl - Ppara - Pnac
Fal = Fa - Pcte - Pnac ou Fal = Fa - Pcte' - Pexpériences avec Pcte' = Pcte + Pnac vide
Fal = Vb. g . ( qair - qhe ) - Pcte - Pnac
4.Ballon en équilibre : Fal = 0 ( ballon immobile )
Pa = Ptotal = Penv + Phe + Prefl + Ppara + Pnac = Pb + Phe
qair. Vb. g = qHe . Vb. g + Pb d'où Pb = qair. Vb .g - qhe . Vb . g = Vb . g ( qair - qhe )
à l'équilibre : le volume d'hélium doit être de
Vb = Pb / g . ( qair - qhe ) = 40 / 9,81 ( 1,200 - 0,166 ) = 3,90 m3 à 20°C
Si le volume d'hélium devient supérieur à cette valeur le ballon va monter avec une certaine vitesse, d'autant plus forte que le volume sera plus fort.
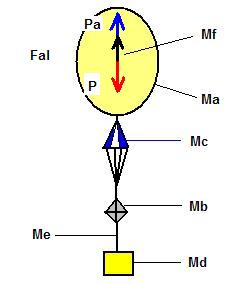 |
Bilan
des forces : ( le centre de gravité n'est pas bien placé).
Fal = Pa - P avec P = somme de tous les poids, y compris celui de l'hélium. Fal = ( Pa - Phe ) - Pb ( Pb : somme de tous les poids sauf celui de l'hélium ) Fal = qair . Vb. g - qhe . Vb . g - Pb ( qair et qhe : densités et g = 9,81 ) Fal = ( qair - qhe ) . Vb . g - Pb ( Vb : volume d'hélium ) Fal = ( 1,2 - 0,166 ) . Vb . g - Pb à 20°C Fal = ( 1,034 ) . 9,81 . Vb - Pb = 10,14 . Vb - Pb |
Or nous avons fait un choix pour la vitesse limite de montée de 5 m/s, le tableau de la page précédente donne pour cette valeur Fal = 17 N.
On peut écrire : Fal = 10,14 . Vb - 40 = 17 d'où on tire la valeur du volume Vb = 57 / 10,14 = 5,624 m3 d'hélium, soit 5, 7 m3
5.Vérifications:
La poussée d' Archimède est : Pa = 1,2 . Vb . g = 1,2 . 5,7 . 9,81 = 67,1 N ( ou 6,84 kg )
Le poids de l'hélium embarqué est : Phe = 0,166 . Vb . g = 0,166 . 5,7 . 9,81 = 9,282 N ( ou 0,9462 kg )
La force ascensionnelle du ballon est : Fa = Pa - Phe = 67,1 - 9,282 = 57,818 N ( ou 5,894 kg ) c'est la force ressentie en prenant l'enveloppe à la main par son manchon à la base.
La somme de tous les poids sauf celui de l'hélium : Pb = 40 N ( ou 4,08 kg )
La force ascensionnelle libre du ballon est : Fal = Fa - Pb = 57,818 - 40 = 17,818 N soit 18 N ( ou 1,816 kg )
C'est bien la valeur souhaitée au départ pour obtenir la vitesse limite de 5 m/s à partir du tableau des Fal.
On peut écrire : Fa = 10,14 . Vb et Fal = Fa - Pb Fal = 10,14 . Vb - Pb
d'où Vb = ( Fal + Pb ) / 10,14
Vb = ( 17 + 40 ) / 10,14 = 5,7 m3
Il suffit de connaître le poids du ballon ( tout sauf hélium ) : Pb, et de choisir la Fal pour la vitesse souhaitée ( au choix 4 ou 5 m/s ).
départ d'un ballon avec nacelle photographique.
photo : Alain F6AGV
enveloppe 1200 grammes : notice constructeur = VALEURS NOMINALES calculées pour une sonde météo classique de 400 grammes qui va monter à la vitesse de 6 m/s. Notre ballon a une charge de 2,5 kg et sa vitesse de montée réelle sera inférieure à cette valeur. Elle sera comprise entre 4 et 5 m/s. Une valeur de 4 m/s est parfaitement acceptable et il ne faut pas vouloir absolument à obtenir la plus forte vitesse de montée car en montant la Fal plus que nécessaire, cela va se traduire par un volume d'hélium prohibitif. Tenir compte de la température et de la pression du point de lancement pour l'hélium injecté dans le ballon et disponible pour chaque bouteille. Une même bouteille ne donne pas un volume constant.
| COSMOPRENE KS 1200 34.5km BALLOON Weather balloon MFG CO. LTD |
| Burst Altitude : 34,500 m |
| Diam -Flacid 127 cm. more |
| Inflated 170 cm. |
| Burst 890 cm. |
| Volume -Inflated 2.6 cu.m. |
| Burst 369 cu.m. |
| Weight 1,200 +- 45 gr. |
| Neck Diameter 3.2 +- 0,4 cm. |
| Length 14 +- 2 cm. |
| Color Uncolored |
| Payload 400 gr. |
| Free Lift 1,500 gr. |
| Rate of Ascent 360 m/min. |
documentation,
bibliographie, ouvrages, livres et articles utilisés pour établir les pages
: ![]()
à
suivre : exemples de calculs pratiques
