 |
BALLON A GAZ (1) |
 |
BALLON HELIUM
ballon de 1200 grammes gonflé à l'hélium, avec parachute et réflecteur.
photo : Alain F6AGV.
L'hélium :
L'hélium existe en abondance dans l'atmosphère du soleil, d'où l'origine de son nom : hélios. On ne le trouve qu'à l'état de traces dans l'atmosphère terrestre. C'est un gaz "rare", un des premiers à avoir été créé. Il est très abondant dans l'univers 25% mais rare sur Terre, car il s'échappe de l'atmosphère et est emmené par les vents solaires. Toutefois, on peut le trouver sous forme fossile dans des poches de gaz naturel de quelques gisements pétroliers dans certaines régions des USA, d'Algérie et de Pologne. On l'extrait alors au moyen de forages profonds dans le sous-sol.
L'hélium est un gaz extrêmement léger et il est par conséquent très volatile. Il est incolore, inodore, ininflammable et complètement inerte. Il n'entretient pas la vie.
Données de conversion pour l'hélium:
| livres ( lb ) | kilogrammes kg | pieds cubes scf | mètres cubes Nm3 | gallons ( gal ) | litres ( l ) | ||
| 1 livre | 1 | 0,4536 | 96,71 | 2,542 | 0,95930 | 3,631 | |
| 1 kg | 2,205 | 1 | 213,2 | 5,603 | 2,115 | 8,006 | |
| 1 scf ( gaz ) | 0,01034 | 0,00469 | 1 | 0,02628 | 0,009919 | 0,03754 | |
| 1 Nm3 ( gaz ) | 0,3935 | 0,1785 | 38,04 | 1 | 0,3775 | 1,4289 | |
| 1 gal ( liquide ) | 1,042 | 0,4728 | 100,8 | 2,649 | 1 | 3,785 | |
| 1 litre ( liquide ) | 0,2754 | 0,1249 | 26,63 | 0,6998 | 0,2642 | 1 | |
Les scf ( pieds cube standard ) de gaz sont mesurés à 1 atmosphère et 70°F. Les Nm3 ( normaux mètres cubes ) de gaz sont mesurés à 1 atmosphère et 0°C. Le liquide est mesuré à 1 atmosphère et à la température d'ébullition.
Propriétés physiques :
| Unités métriques | Unités US | ||
| Symbole chimique | He | He | |
| masse molaire | 4,00 | 4,00 | |
| phase liquide ( point d'ébullition) | densité (eau=1) | 0,124 à 1,013 bar | 0,124 à 1 atm |
| capacité de chaleur massique | 4,545 kJ/kg°C | 1,086 BTU/lb°F | |
| température | -268,9°C à 1,013 bar | -452,06°F à 1 atm | |
| point d'ébullition | chaleur latente de vaporisation | 20,28 kJ/kg | 8,72 BTU/lb |
| densité ( air=1) | 0,139 | 0,139 | |
| phase gazeuse | capacité de chaleur massique | 5,19 kJ/kg°C | 1,25 BTU/lb°F |
| masse volumique | 0,17585 kg/m3 | 0,01114 lb/cu.Ft | |
| température | neant | neant | |
| point triple | pression | neant | neant |
| température | -267,9°C | -450,31°F | |
| point critique | pression | 227 kPa abs | 33 psia |
| masse volumique | 69,64 kg/m3 | 4,347 lb/cu.Ft | |
| conductibilité thermique | 0,1567 W/m °K à 300 K | 0,0906 BTU/ft h °F à 80°F | |
| température de fusion | -272°C à 26 atm ( 1,16 K ) | ||
| température d'ébullition | -268,6°C ( 4,56 K ) | ||
| vitesse du son | 970 m/s | ||
| indice de réfraction/air | 1,000 035 |
Volume d'hélium :
pour l'air : l'air pèse 29 grammes par mole. Une mole occupe 22,4 litres ou 22,4 dm3 au niveau du sol. Il y a 6,023 . 1023 molécules par mole.
La masse de l'air par mètre cube est : 29 / 0,0224 = x / 1 soit 1294,64 g / m3 ou 1,294 kg / m3 ( 28,964 grammes pour l'air sec ).
Le poids de l'air par mètre cube est : 1,294 . 9,81 = 12,68 N / m3
pour l'hélium : l'hélium pèse 4 grammes par mole.
La masse de l'hélium par mètre cube est : 4 / 0,0224 = x / 1 soit 178,6 g / m3 ou 0,1786 kg / m3
Le poids de l'hélium par mètre cube est : 0,1786 . 9,81 = 1,752 N / m3
Poussée d'Archimède : Si on considère une mole d'air sec, sa masse est de 29 grammes. Si on considère une mole d'hélium, sa masse est de 4 grammes. En application du théorème, la poussée verticale sur la masse d'hélium est égale à la masse d'air qui occupe le même volume, c'est à dire 29 grammes x g . Cette poussée est dirigée vers le haut, or pour la masse d'hélium, son poids est dirigé vers le bas, c'est à dire 4 grammes x g .
On peut dire que la force ascensionnelle de l'hélium est de : 25 grammes par mole d'hélium. Ou on peut dire aussi que pour soulever 1 000 grammes, il faut 40 moles d'hélium. Mais la charge sera comprise entre 0 et 25 grammes, la vitesse de montée sera nulle pour 25 grammes puisque 29 - ( 25 + 4 ) = 0 .
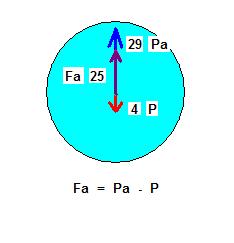 |
 |
 |
A gauche : 25 . g = 29 . g - 4 . g ( g = gravité 9,81 ) on ne tient pas compte de la présence d'une enveloppe autour de l'hélium.
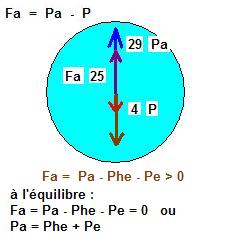
Au milieu : Fa = Pa - Phe - Pe La force ascensionnelle Fa est la résultante de la poussée d' Archimède Pa ( dirigée vers le haut ) et de la somme des poids de l'hélium Phe et de l'enveloppe Pe ( dirigés vers le bas ). A l'équilibre, il y a égalité et Pa est équilibré par Phe + Pe, mais le ballon ne peut s'envoler.
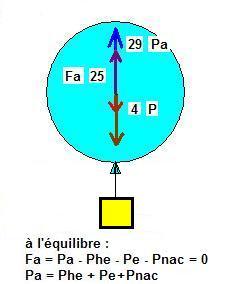
A droite : Fa = Pa - Phe - Pe - Pnac on peut écrire la condition de décollage : Pa > Phe + Pe + Pnac ( Pnac = Pnacelle )
Force ascensionnelle libre : Fal c'est la résultante appliquée sur l'ensemble du ( ballon + charge ) et en vol au décollage.
Pour la suite des calculs, on va poser Fa = (Pa - Phe) ( voir dessin à gauche ). Pour une mole, ou un volume de 22,4 litres d'hélium, on aura Fa = 0,025 . 9,81 = 0,24525 N. ( ou 25 grammes ).
Pour 40 moles ou un volume de 40 . 22,4 dm3 d'hélium = 896 dm3 ou 0,896 m3 on aura Fa = 0,24525 . 40 = 9,81 N ( ou 1 kg ).
Cela veut dire que ce volume d'hélium peut soulever une masse de 1 kg au maximum. La charge totale sera comprise entre 0 et 1 kg, avec une charge de 1 kg il y aurait équilibre, donc pas de mouvement. Pour une charge supérieure à 1 kg, évidemment il y aurait impossibilité de décollage.
Avec un volume de 1 m3 d'hélium, il serait possible de soulever au maximum : 1 / 0,896 = x / 9,81 d'où Fa = 9,81 / 0,896 = 10,9487 N ( ou 1,116 kg ).
Donc, la valeur de Fa ou force ascensionnelle va dépendre de la quantité d'hélium présente dans l'enveloppe ainsi que la vitesse de montée.
Pour la suite des calculs on écrira : Fal = ( Pa - Phe ) - Pe - Pnac = Fa - Pe - Pnac
Tableau des valeurs des forces ascensionnelles libres : établi par Planète-Sciences pour une nacelle de 1,5 à 2,5 kg + parachute et divers de 0,4 kg.
Nous n'avons pas vérifié ces valeurs expérimentalement, et nous choisissons de nous baser uniquement sur les calculs de physique.
| masse de l'enveloppe | vitesse de montée : 4 m/s | vitesse de montée : 5 m/s |
| 600 g | 9 N ( ou 0,9174 kg ) | 15 N ( 1,529 kg ) |
| 1000 g | 10 N ( ou 1,019 kg ) | 16 N ( 1,63 kg ) |
| 1200 g | 10 N ( ou 1,019 kg ) | 17 N ( 1,733 kg ) |
| 2000 g | 11 N ( ou 1,121 kg ) | 18 N ( 1,835 kg ) |
premier exemple de choix du volume d'hélium :
Pour simplifier et rendre les calculs pratiques, volontairement les forces en N seront en fait exprimées par des masses en kg !
Nous fabriquons un ballon avec un mole de gaz ( 22,4 litres d'hélium ou 22,4 dm3 ) et ensuite on s'occupera du ballon réel.
Comme il est indiqué ci-dessus, la force ascensionnelle Fa de ce "ballon-mole" sera de 29 grammes - 4 grammes = 25 grammes.
Le ballon-mole peut soulever une charge de 25 grammes, mais c'est un maximum ! Et sa vitesse de montée serait quasi nulle pour la charge maximale de 25 g.
Pour soulever 1000 grammes, le raisonnement est le même, il faudrait 1000 / 25 moles de gaz, soit 40 moles. Le volume d'hélium serait alors de 40 . 22,4 dm3 , soit un volume de 0,9 m3 pour soulever 1 kg au maximum. Mais la vitesse de montée serait quasi nulle avec la charge maximale.
La poussée d'Archimède Pa est de 29 g x 40 = 1160 g ou 1,16 kg.
Le poids de l'hélium PHe ( exprimé en kg ! ) est de 4 g x 40 = 160 g ou 0,116 kg.
La force ascensionnelle Fa ( = charge maximale possible ) est 25 g x 40 = 1000 g ou 1kg.
Si le "ballon 40 moles" soulève une charge utile entre 0 et 1kg, la force ascensionnelle LIBRE sera égale à Fa - le poids de la charge utile PsHe.
Fal = Fa - PsHe ( charge utile est appelée Poids sans hélium ).
Le poids sans hélium comprend le poids de l'enveloppe du ballon et la charge expérimentale située dans une nacelle, plus des accessoires.
Si PsHe = Fa la Fal est nulle et la ballon ne peut pas décoller, si il est déjà en l'air alors il reste à la même altitude.
Si PsHe > Fa la Fal est négative et le ballon ne peut absolument pas décoller ou il chute.
Si la Fal est positive le ballon monte plus ou moins rapidement.
On peut choisir une valeur de la Fal par expérimentations successives et en déduire la vitesse de montée. Un tableau ou une abaque sera fournit pour aider au choix préalable au vol.
Dans cet exemple, le choix se fait pour une Fal de 1,6 kg ( toujours en kg ! ). On espère une vitesse de montée de 4 à 5 m/s au décollage et pendant la première partie du vol de 0 à 30 000 mètres jusqu'à l'éclatement de l'enveloppe.
Pa - PHe - PsHe = Fal ( bilan des forces appliquées au centre de gravité du ballon )
Si PsHe est au maximum possible on a : Pa - PHe - PsHe = 0
Si PsHe est au minimum, c'est le poids de l'enveloppe Penv on a : Pa - PHe - Penv = Fal
Pour faire voler le ballon et le faire monter, il faut Fal > 0 et PsHe < ( Fa )
Si le facteur PsHe est imposé ( bilan des masses ) : Fal = Fa - PsHe
Il faut CHOISIR la Fal suivant la vitesse souhaitée : donc le moyen de réglage se trouve dans le facteur Fa force ascensionnelle.
On ne peut intervenir que sur le volume de l'enveloppe et les masses volumiques. En plus ces valeurs changent en fonction de l'altitude naturellement.
Dans cet exemple, le choix se porte sur Fal = 1,6 kg en fonction de critères expérimentaux et conditionne la valeur de la vitesse de montée. Le constructeur fabrique des ballons Latex pour les valeurs optimum et une utilisation bien précise avec de sondes météo RS80 de 400 grammes. Il préconise une Fal de 1,5 kg, cette valeur est NOMINALE.
Il n'est pas obligatoire de choisir exactement cette valeur NOMINALE, car la charge utile ne sera pas la même ( 1 à 2,5 kg maximum au lieu de 0,4 kg ). La vitesse de montée ne sera pas la même ainsi que l'altitude de l'éclatement qui ne sera pas NOMINALE non plus.
Seule la feuille de calcul basée sur les formules de physique et les données atmosphériques peut résoudre le choix proposé. Donc la Fal est fixée à 1,6 kg mais cette valeur peut varier entre deux limites estimées de 1,5 à 2,5 kg.
Fa = Fal + PsHe = 1,6 + 4,08 = 5,68 kg ( à 0°C ) avec Fa = Rhoair0 . V - RhoHe0 . V ( sans g ! )
Fa = V . ( Rhoair0 - RhoHe0 ) = V . ( 1,29 - 0,1784 ) = V . 1,1116 d'où V = 5,11 m3
Hélas, le calcul de la vitesse prouve que le volume n'est pas suffisant, et il faut tenir compte de la température et de la pression atmosphérique aussi bien pour le gonflage du ballon et pour les bouteilles d'hélium. Les différences ne sont pas énormes mais si on cherche à calculer la trajectoire et à faire des prévisions sur le point de chute, il serait ridicule de ne pas maîtriser la valeur du volume d'hélium qui est un des seuls paramètres du vol modifiable par le lanceur du ballon.
En plus, il est important d'avoir une démarche scientifique et de ne pas négliger la précision quand il est possible d'éviter des erreurs. Tout le vol est modélisé depuis le point de départ jusqu'au point de chute, l'éclatement sera programmé en fonction des prévisions de trajectoire et le point de chute choisi à l'avance en fonction des vents. ( voir TRAJECTOIRE ).
Les
conditions météo sont de 20°C et 1010 hPa au jour du lancement et la Fal
est majorée ( voir feuille de calcul Excel :  ) à 2 kg.
) à 2 kg.
Nouvelles valeurs :
Fa = 2 + 4,08 = 6,08 kg
Fa = V ( 1,2 - 0, 167 ) = V . 1,033 d'où V = 5, 89 m3
Le
volume est passé de 5,11 ( à 0°C ) pour 5,89 m3
( à 20°C ). Une valeur serait supérieure en cas de forte
chaleur, voir les différentes possibilités avec la feuille de calcul Excel :
 .
.
Avec une Fal de 2,5 kg : Fa = 2,5 + 4,08 = 6,58 kg
V = 6,58 / 1,033 = 6,37 m3
Conclusion : la fourchette pour le choix du volume est assez large, il n'y a pas une seule valeur possible mais un choix fonction des conditions météo au jour J.
Dernière chose : pour une pression mesurée sur la bouteille de 180 bars, le volume disponible injecté dans le ballon sera fonction de la pression atmosphérique et de la température ambiante, il n'y a pas une valeur unique par exemple de 2,7 m3 pour une B15. Il n'est pas difficile d'apporter une correction très simple, cela fait aussi parti de la démarche scientifique. ( voir REMPLISSAGE ).
La précision du manomètre ne sera pas toujours bonne, vu l'appareil et son état réel, alors le tarage ou l'emploi d'un dynamomètre sera indispensable, si on ne veut pas remplir le ballon avec n'importe quel volume. ( voir REMPLISSAGE ).

photo : Alain F6AGV
documentation,
bibliographie, ouvrages, livres et articles utilisés pour établir les pages
: ![]()