poussee_d'archimede

sommaire

POUSSEE D'ARCHIMEDE (1)

POUSSEE D'ARCHIMEDE

photo : Alain F6AGV

ballon de baudruche parfaitement immobile en équilibre entre sol et plafond :

réglage par le découpage du papier sur les coins avec des ciseaux au fur et à mesure des pertes d'hélium.

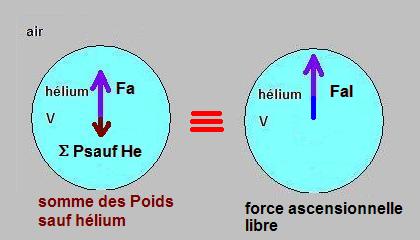
Le ballon reçoit une poussée dirigée de bas en haut : Pa , c'est la poussée d'Archimède ( dessin à gauche ).

Cette force est égale au poids du même volume d'air extérieur V : Pair ( dessin au milieu ).

Le ballon est rempli de gaz plus léger que l'air : par exemple de l'hélium ( gaz rare ). Pourquoi ?

Le poids du gaz contenu dans le volume V doit être inférieur au poids de l'air qui occuperait le même volume. ( dessin à droite ).

Un ballon remplit avec de l'air ne pourrait pas voler, il faut que la différence de poids : ( Pair - Pgaz ) soit positive et non nulle.

Comparez les dessins de gauche et de droite : deux forces sont appliquées au centre de gravité du ballon.

En effet ( Pair - Pair ) = 0 ne pourrait pas faire décoller le ballon.

Quel est le poids de l' air contenu dans un volume Vb donné : c'est

Rhoair : masse volumique de l'air en kg / m³ , Vb : volume du ballon en mètre cube, g = 9,81 m/s²

C'est cette force Pa qui est appelée la poussée d'Archimède.

Le poids de l'hélium dans le même volume Vb est :

RhoHe : masse volumique de l'hélium en kg / m³ .

Le choix du gaz est important, c'est à dire sa masse volumique. Pour l'hélium dans les conditions normales ( 0°c et 1013,25 hPa ), la valeur est de 0,1785 kg / m³ . Pour l'air dans les mêmes conditions, la valeur est de 1,29 kg / m³ . Avec l'emploi de ces deux gaz, la différence des poids est bien positive.

On a ( Rhoair - RhoHe ) > 0 cela veut dire que le ballon peut voler et :

Le ballon est donc soumis à deux forces : ( sans compter l'enveloppe )

la poussée d'Archimède Pa et le poids de l'hélium :

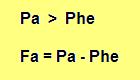
Exemple de calculs :

Le volume du ballon est de 6 m³ Vb = 6 m³

La masse volumique de l'air est Rhoair(o) = 1,29 kg / m³

La masse volumique de l'hélium est RhoHe(o) = 0,1785 kg / m³

287,053 est la constante relative à l'air sec = 1 . 8,31432 / 0,028964 = 287,05 J/kg/K

2078,58 est la constante relative à l'hélium = 1 . 8,31432 / 0,00400 = 2078,58 J/kg/K

Pa = 1,29 . 6 . 9,81 = 76,06 N

Phe = 0,1785 . 6 . 9,81 = 10,50 N La force ascensionnelle FA est 76,063 - 10,5065 = 65,5565 N

Recommencez le calcul avec T°C = 15 °C et 1010 hPa.

Autre problème un peu plus théorique: on exprime les valeurs en masse et non en poids.

Le ballon est gonflé avec une "mole" d'hélium ( c'est à dire 22,4 litres ou 22,4 dm³ d'hélium ). Une mole d'hélium a une masse de 4 grammes.

La poussée d'Archimède sera donnée par la masse de l'air qui occupe 22,4 litres de volume, c'est à dire une mole d'air. Une mole d'air a une masse de 29 grammes. ( en réalité c'est : 28,964 grammes compte tenu de tous les constituants de l'air ).

La force ascensionnelle Fa est : 29 - 4 = 25 grammes pour une mole d'hélium ou 22,4 dm³

La force ascensionnelle Fa pour 1 m³ est 25 / 0,024 = 1 116 grammes soit 1,116 kg pour 1 m³ d'hélium.

Ou on peut dire que pour soulever 1 kg, il faut 1 / 1,116 m³ c'est à dire : 0,896 m³ soit 0,9 m³

Mais si on veut soulever exactement 1 kg, avec 0,9 m³ : la vitesse de montée sera nulle ! On peut soulever une charge de 0 à 1 kg maximum.

La vitesse de montée sera fonction de la valeur de la charge donc de la force ascensionnelle Fa.

Combien de moles faut-il pour soulever 1 kg ?

R : 896 / 22,4 = 40 moles.

La force ascensionnelle est dirigée vers le haut et il y a une force qui s'oppose à la montée, c'est la résistance du vent ou frottement qui s'appelle "la traînée" en aviation ou en aérostation :

Remarque importante : il y a égalité entre Fa et T pendant le vol du ballon. La force ascensionnelle est égale à la traînée.

De ce fait, la vitesse de montée peut être calculée avec une relation :

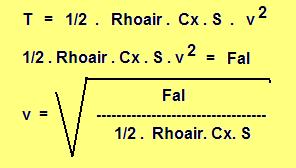
Cx : coefficient de traînée égal à 0,5 pour une sphère.

S : surface diamétrale ou maître couple en m ²

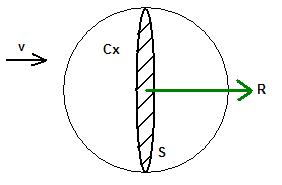
v : vitesse de déplacement en m/s

Fal : force ascensionnelle libre, voir plus bas.

La FORCE ASCENSIONNELLE LIBRE : Fal

Un ballon n'est pas composé uniquement de gaz hélium, il lui faut une enveloppe pour contenir le gaz, sinon il partirait dans l'atmosphère et se perdrait dans l'espace et le vide spatial.

L'enveloppe doit être résistante, élastique, légère et non poreuse. En réalité l'enveloppe est plus ou moins poreuse, ce qui explique que les ballons de baudruche tombe rapidement sans cause apparente : l'enveloppe est réellement microporeuse !

Une montgolfière à air chaud devient poreuse au bout de 400 ou 500 heures de vol. Mais la consommation de propane pour la chauffer augmente au fur et à mesure, ce qui augmente le coût d'exploitation et les montgolfières sont vendues en occasion ou réformées.

En plus de l'enveloppe pour contenir l'hélium, le ballon a pour mission d'envoyer une charge utile dans l'espace, il y a aussi des accessoires comme un parachute et un réflecteur radar pour la localisation par l'aviation. Il faut donc tenir compte de tous les poids dans le calcul de la FORCE ASCENSIONNELLE.

On l'appellera donc la FORCE ASCENSIONNELLE LIBRE : Fal

On voit bien que la Fal est réduite par rapport à la force ascensionnelle Fa, puisqu'il faut soustraire des poids supplémentaires. Il faut donc chercher à réduire les poids inutiles et à alléger au maximum toutes les parties annexes du ballon.

On utilisera pour la fixation un "cure-dent" plutôt qu'un boulon de 5 mm en acier, du ruban adhésif et de la colle, et du carton plutôt que de la plaque aluminium ! ( pour les petits ballons ).

Règle : réduire le poids des accessoires pour augmenter le poids des expériences embarquées...

Dans le cas où la somme des poids supplémentaires serait égale à Fa, alors la Fal serait nulle. Le ballon serait immobile ou garderait son altitude. Un ballon au sol avec une Fal nulle ou insuffisante ne peut pas décoller ou très mal. On risque de la projeter sur des obstacles au sol.

En vol, une montgolfière va modifier constamment sa Fal, l'augmenter ou la réduire pour pouvoir monter ou descendre et finalement prendre les bons vents dans les bonnes couches d'air. Cas particulier : la Fal est nulle.

Comment faire pour augmenter la Fal ?

Il faut augmenter Fa, ou diminuer les poids. C'est une technique utilisée par les aérostiers qui lâchent du "lest" en vol ( sable ). Ce lest est embarqué au départ et destiné à faire monter le ballon quand il le faut. Mais la réserve s'épuise alors il faut atterrir.

On peut aussi soupaper le gaz, donc diminuer Fa pour descendre.

Avant le lâcher d'un ballon à l'hélium, on peut CHOISIR la Fal pour obtenir une vitesse de montée ou une altitude précise AU FINAL, en jouant sur le volume de gaz hélium injecté initialement.

Pendant le vol, on peut régler la Fal en jouant sur le volume de gaz, en évacuant l'hélium avec une soupape ( descente ). On peut régler le volume de gaz ou de l'enveloppe, agir sur la différence des masses volumiques avec l'emploi de l'air chaud à la place de l'hélium ( montée ou descente ), ou bien lâcher du lest ( montée ). Les ballons mixtes hélium - air chaud ( Rosières ) ont plus de possibilités pour monter ou descendre.

Si l'enveloppe d'un ballon hélium éclate alors il n'y a plus le terme Fa, il ne reste que les poids : c'est la chute libre freinée par un parachute.

Le problème du parachute c'est qu'il doit fonctionner parfaitement pour garantir une vitesse de descente modérée et une possibilité de modélisation du point de chute. A défaut de parachute efficace, c'est la nacelle (et le réflecteur radar ) qui contribue au freinage, la surface ou maître couple de la nacelle doit être non négligeable.

Dans le cas des ballons à air chaud :

L'air chaud à 200°C a une masse volumique de 0,746 kg / m³ .

La température de l'air chaud ne dépasse pas les 100°C dans les montgolfières et 50°C dans les ballons solaires. On peut modifier l'altitude en chauffant plus ou moins l'air chaud ou de façon périodique, et laisser se refroidir l'air pour la descente. Une soupape permet aussi de laisser échapper l'air chaud pour provoquer la descente. Un ballon qui se refroidit totalement voit sa force ascensionnelle Fa nulle, dans ce cas le ballon se trouve en chute libre ! Solution utilisée par les montgolfières juste avant l'atterrissage en ouvrant un panneau ou une soupape au sommet.

Exemple numérique :

Vb = volume du ballon hélium = 6 m³

Rhoair = 1,29 kg / m³ , RhoHe = 0, 1785 kg / m³

Masse de la nacelle : 2,5 kg Pnacelle = .......

Masse de l'enveloppe : 1,2 kg Penveloppe = .......

Masse de la charge utile : ( comprise dans la nacelle )

Masse des accessoires : 0,26 + 0,12 + 0,1 Pacc = .......

Somme des masses sauf hélium : 4,18 kg Psauf hélium = ......

Trouvez la Fal et la vitesse de montée ?

Fal = 9,81 . 6 . ( 1,29 - 0,1785 ) - 4,18 . 9,81 = 65,556 - 41 = 24,55 N

Le ballon étant en vol avec cette valeur de Fal, la traînée aura la même valeur de 24,55 N.

La traînée pour une sphère est de la forme :

r = 1,127 m et D = 2,254 m S = 0,7854 . ( 2,254 )² = 3,99 m² # 4 m² et la vitesse de montée = 4,36 m/s

autre calcul :

--- température de 20°C

--- pression de 1010 hPa

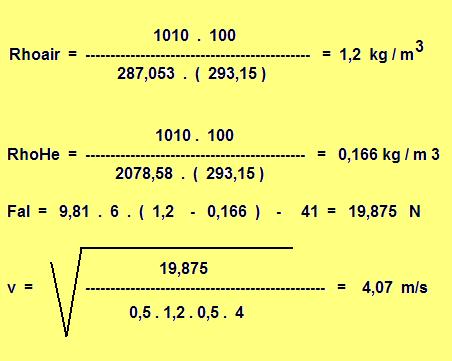
autre remarque : le ballon va monter jusqu'à son altitude qui correspond à son éclatement naturel ( burst ). Le diamètre de l'enveloppe à son éclatement est de 8,9 m pour le type 1200 grammes.

Les valeurs comprises dans la formule de la Fal changent en fonction de l'altitude, de la température et de la pression. On placera un indice z sur les variables qui varient avec l'altitude. La vitesse de montée ne change pas beaucoup pendant le vol. Nous la fixons à la valeur de 5 m/s, mais une valeur de 4 m/s est possible également.

documentation, bibliographie, ouvrages, livres et articles utilisés pour établir les pages :

à suivre,