droite

sommaire

DROITE

EQUATION D'UNE DROITE :

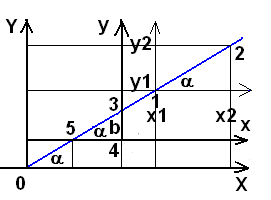
Premier repère d'origine Y, 0, X :

forme générale : ci-dessus la droite en bleu qui passe par les points 0,5,3,1 et 2.

échelle ou axe des Y : ordonnées

échelle ou axe des X : abscisses

a est un coefficient appelé pente, c'est aussi la dérivée y' de y et la tangente en un point.

La tangente est le rapport des longueurs des côtés du triangle rectangle : opposé sur adjacent.

tan α =

La droite passe par l'origine au point 0 : coordonnées x = 0 et y = 0

Il faudrait écrire pour exprimer la tangente : tan α =

exemple 1 : on donne x1 = 11 et y1 = 5 sur le premier repère Y, 0, X.

écrire l'équation de la droite en littéral et en numérique avec les chiffres proposés ?

Ensuite on donne x2 = 15 calculer y2 avec l'équation trouvée ?

Solution : y = x y = x y = 0,4545 . x

pour x2 = 15

y2 = 0 ,4545 . x2 = 0,4545 . 15 = 6,8181

exemple 2 : écrire l'équation de la droite connaissant deux points 1 et 2 ? Voir figure.

Les données sont x1, y1 et x2, y2 dans le premier repère Y, 0, X.

La forme générale de l'équation est toujours y = a . x

Solution :

tan α = = = 0,4545 (la pente est la même!)

l'équation de la droite est :

y = . x = 0,4545 . x (équation inchangée)

exemple 3 : le point 1 est déclaré comme origine, calculer y2 suivant les axes nouveaux ?

Solution : y = 0,4545 . x avec x2 = 15 - 11 = 4 par rapport au point 1.

y2 = 0,4545 . x2 = 0,4545 . 4 = 1,8181

exemple 4 : l'origine n'est plus au point 1 mais au point 4 situé en dehors de la droite.

Les axes y et x sont tracés à partir du point 4.

Par rapport au repère d'origine, (le tout premier) : x4 = 9 et y4 = 2 Voir figure.

La droite en bleu coupe le nouveau repère en deux points : un point 3 sur l'axe y

et un point 5 sur l'axe x.

Par rapport au nouveau repère dont l'origine est au point 4, calculez les coordonnées

x et y des points 1 et 2 ? C'est à dire : x1, y1 et x2, y2

Solution :

x1 = 11 - 9 = 2 y1 = 5 - 2 = 3

x2 = 15 - 9 = 6 y2 = 6,8181 - 2 = 4,8181

exemple 5 : l'origine est toujours au point 4 et la droite ne passe pas par ce point.

Les données sont les points x1, y1 et x2, y2 et les valeurs calculées à l'exemple 4.

Exprimez et calculez la pente tangente α en fonction de x1, y1 et x2, y2

Ensuite exprimez en littéral sans calculer la pente tangente α en fonction de

x2, y2 et x3, y3 ?

Vous ne connaissez pas la valeur de y3.

Vous la calculez en fonction de tan α, x2, y2 et x3, y3 !

Solution :

tan α = Calcul : tan = 0,4545 ( même pente )

tan α = On remarque que x3 est nul et on connait tan α

tan α . x2 = y2 - y3 ---> y3 = y2 - ( tan α . x2 )

y3 = 4,8181 - ( 0,4545 . 6 ) = 2,0911

exemple 6 : A partir de l'exemple 5, exprimez y3 en littéral en fonction de

x1, y1 et x2, y2 sachant que x3 = 0

Solution :

tan α = =

(y2 – y1) . ( x2) = (y2 – y3) . (x2 – x1) l'inconnu est y3 !

y2.x2 - y1.x2 = y2. x2 - y3. x2 – x1 . y2 + y3 . x1

x1 . y3 - x2 . y3 = x2 . y2 - x2 . y1 - x2 . y2 + x1 . y2

y3 ( x1 - x2 ) = x1 . y2 - x2 . y1

y3 = on multiplie par -1 en haut et en bas

y3 =

exemple 7 : A partir du résultat précédent à l'exemple 6, calculez la valeur de y3 ?

Solution :

y3 = = 2,09

exemple 8 : La valeur y3 sera appelée b

Nous connaissons l'équation d'une droite de la forme y = a . x

ou y = tan α . x = . x

Calculez la pente et donner l'équation ?

Calculez y2 avec l'équation et x2 = 6 ?

Solution :

y2 = 0,4545 . 6 = 2,727 ce qui n'est pas correct car dans l'exemple 4 , on avait trouvé

y2 = 4,8181

Tout ce passe comme ci, la droite passait par le point 4 avec la même pente !

Elle serait parallèle à la droite en bleu ! Pour trouver y2, c'est à dire les coordonnées du point 2

( x2 = 6 et y2 = 4,8181) il faut ajouter à l'équation de y la valeur du décalage entre les droites ,

la bleue et la droite parallèle qui passe par le point 4.

Le décalage est y3 ou b et l'équation devient y = a . x + b

pour x2 = 6

y2 = 0,4545 . 6 + 2,0911 = 4,8181

L'équation d ' une droite connaissant deux points x1, y1 et x2, y2 est :

y = . x +

Application : y = 0,4545 . x + 2,0911

exemple 9 : Donner l'expression de x5 pour le point 5 de la droite quand y5 = 0

et calculez x5 ?

Solution :

0,4545 . x5 + 2,0911 = 0 d 'où x5 = - = - 4,6

on pouvait écrire :

( y2 - y1 ) . x5 = y2 . x1 - y1 . x2

x5 = = - 4,6

---------------------------------------------------------------

écrit par Alain F6AGV - BHAF - 240114

documentation, bibliographie, ouvrages, livres et articles utilisés pour établir les pages :

à suivre,