baromètre_à_eau_application

sommaire

BAROMETRE A EAU CALCULS

BAROMETRE A EAU : application numérique et feuille de calculs Excel

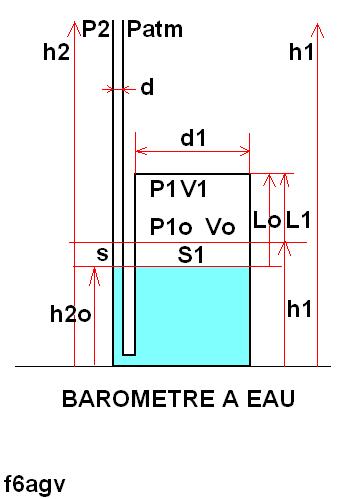
Configuration de base :

Le baromètre à eau se compose de trois parties :

le réservoir principale ou flacon qui est fermé et transparent. Diamètre d1.
le tube sur le côté de faible diamètre d ou d2. Ouvert au sommet, à l'air libre.
la liaison entre le flacon et le tube. On négligera cette partie dans les calculs.

Conditions initiales :

Le flacon a été rempli de liquide coloré. (eau + colorant). Sur la photo du baromètre, vous verrez

un liquide bleu qui est utilisé pour le refroidissement des moteurs, donc qui ne craint pas le gel.

Le niveau initial est h2o ou h1o. En principe identique des deux côtés, mais ce n'est pas impératif au remplissage. Il faut juste respecter un volume de liquide connu : qui sera

V liquide = S1 . h1o + S2 . h2o

Avec S = pi . ( r^2 ) et S1 = pi . (r1^2 ) prendre pi = 3,141632

Le volume initial de l'air dans le flacon fermé est : Vo = S1 . Lo et la pression atmosphérique au moment du remplissage est P1o.

--- noter P1o et la température au moment du remplissage To en °C

On peut vérifier que : avec R = 8,314 J/K.mol c'est une constante.

T en kelvin = T en °C + 273,15

V1o : Vo initial volume en m^3

n : nombre de moles d'air

P1o : en pascal Pa

Loi des gaz parfaits :

Un gaz considéré comme parfait vérifie les lois suivantes :

Loi de Mariotte : P . V = cte

Lois de Gay Lussac :

On peut rassembler ces trois lois en une seule :

Loi des gaz parfaits :

Les météorologues préfèrent ne pas s'occuper du volume et utilisent la loi des gaz parfaits sous la forme qui introduit la masse volumique d'une particule :

P = rho . R . T (1)

avec R = Ra qui est la constante des gaz parfaits appliquée à l'air sec.

P = rho . Ra . T (2)

P : pression en pascal Pa

T : température en kelvin K

rho : masse volumique en kg/m^3 avec rho = la masse étant unitaire.

Autre forme :

P . V = n . R . T

avec R = constante universelle indépendante du gaz = 8,31432 J/mole/K

n : nombre de moles de gaz

Comme rho = on déduit

d' où P . = n . R . T ou P = rho . . R . T

On avait écrit plus haut (1) que : P = rho. Ra . T (2)

on déduit que Ra = . R

Calcul de Ra pour l'air sec : On sait qu'une mole d'air sec ( n = 1 ) a une masse de 28,964 g

Ra = = 287,057 J/kg/K

Volume molaire : la masse d'une mole d'air sec est égale à m = 0,028964 kg/mole

la masse volumique est égale à rho = et

soit 1,293 kg/ m^3 à 0°C donc V = = 0,0224 m^3 / mole

ou 22,4 dm^3 ou 22,4 litres par mole

Si la température est autre que 0°C : rho =

Exemple pour une température de 20°C : kg / m^3

rho = = 1,20478 kg / m^3

V20 = = 0,02404 m^3 / mole ou 24 litres / mole

Nombre de mole dans le flacon : le volume initial est Vo à T°C = 20°C

n = = …...

Application numérique :

Elle est faite en utilisant le tableur EXCEL : télécharger l'application

BAROMETRE_A_EAU_170214.xls :

Les zones en couleur bleu pâle peuvent être modifiées avec d'autres valeurs.

Les valeurs utilisées correspondent à une pression atmosphérique de 1013,25 hPa.

Vous devez ajuster le niveau dans le tube pour qu'il correspond au niveau dans le flacon de façon à ce que h2o = h1o

Suivre la démarche, conservez le tableau d'origine et renommer votre propre application :

entrez :

r rayon du tube : 2 mm

r rayon du flacon : 45 mm

niveau du tube : h2o 60 mm

P2o = Patmo = 101325 Pa

Lo hauteur de l'air dans le flacon : 60 mm

masse volumique du liquide pour l'eau : 995,5 kg/ m^3 ( à 4°C 999,973 kg/m^3 )

accélération pesanteur locale : g = 9,81 m/s^2 variable suivant le lieu et l'altitude.

h2 niveau du liquide dans le tube qui est la variable de l'application en mm

résultats intermédiaires en couleur jaune paille :

section du tube : s mm^2

section interne au flacon : S1 mm^2

volume initial de l'air dans le flacon : Vo en mm^3

entrez :

T : température ambiante en °C

résultats intermédiaires :

T en K

masse volumique de l'air à T°C

nombre de mole : n

n =

n = = 0,01586 mole

n =

résultats intermédiaires :

Vo volume d'air initial mm^3

P1o pression initiale dans le flacon en Pa

h2o – h2 différence de niveau dans le tube si Patm varie en mm

s . ( h2o – h2) volume dans le tube déplacé (du tube vers le flacon ou l'inverse) mm^3

h1 niveau correspondant au déplacement dans le flacon mm

x = (h2 - h1) différence de niveau tube / flacon mm

h1 - h2o différence de niveau dans le flacon mm

L1 = Lo – (h1 – h2o) hauteur d'air dans le flacon après déplacement mm

V1 volume d'air dans le flacon après déplacement mm^3

P1 pression de l'air dans le flacon après déplacement Pa

rho . h1 . g pression hydrostatique dans le flacon

rho . h2 . g pression hydrostatique dans le tube

P2 = Patm pression atmosphérique qui est fonction de h2 Pa

Patm en hPa

Vt volume de liquide à injecter dans le baromètre au total (tube + flacon) mm^3

P1 pour vérification Pa

Patm - P1 différentiel de pression

P1o . Vo comparé à P1 . V1 pour vérification de P.V = cte

Résultats et graphiques de l' application : on cherche à connaître Patm = f ( h2 ) ou Patm = f ( x )

écrit par Alain F6AGV pour le BHAF

documentation, bibliographie, ouvrages, livres et articles utilisés pour établir les pages :

à suivre,