archimede_torricelli

sommaire

ARCHIMEDE et TORRICELLI

ARCHIMEDE et TORRICELLI :

Rappel sur l'expérience de Torricelli :

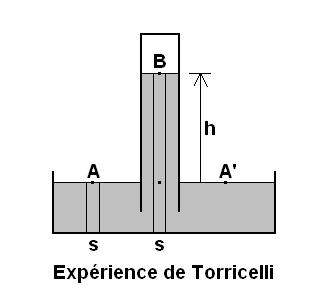
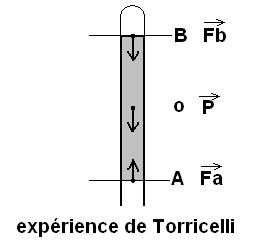
L'élément de liquide (ou colonne ) est en équilibre dans l'éprouvette, et on avait écrit :

Fb + P + Fa = 0 P est le poids de l'élément de liquide

Comme au dessus du point B, il y a le vide (voir expérience de Torricelli), il n'y a pas de pression sur la surface S : l'équation devient

0 + rho . V . g - pa . S = 0 car P = m . g et rho =

et V = S . h d'où :

rho . S . h . g - pa . S = 0 La pression au point A est égale à la pression atmosphérique patm

patm = rho . h . g

avec rho : la masse volumique du liquide en kg/ m^3

h est la hauteur de l'élément en m

g = 9,81 m/s^2

Exemple : h = 0,76 m et le liquide est du mercure avec 13600 kg /m^3

patm = 13600 . 0,76 . 9,81 = 101396,16 Pa ou 1013,9616 hPa

Nous avons fabriqué un baromètre absolu qui peut servir de référence. Des perfectionnements permettent de rendre la lecture plus précise : avec un vernier, on arrivait à une lecture au 1/10 ou au 1/20 de millimètres.

Conversion des centimètres de mercure en hPa :

La pression atmosphérique normale est 101325 Pa

La masse volumique dépend de la température :

http://fr.wikipedia.org/wiki/Masse_volumique

On choisira une valeur de 13545,88 kg/m^3 à 20°C

L'accélération de la pesanteur est donnée pour 9,80665 m/s^2

h sera : h = = 0,76276 m

La pression est donnée en centimètres sur les anciens baromètres :

pcm = phPa . 0,7527855

phPa = pcm . 1,3283995

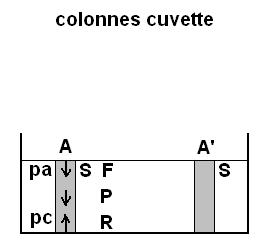
Pour un élément de liquide dans la cuvette de l'expérience de Torricelli, en équilibre, nous avons écrit l'équation des forces et du poids :

F + P = R

F est égal à la pression atmosphérique pa x surface de la section de l'élément S

P est égal au poids de l'élément de liquide

R est égal à la réaction du fond de la cuvette contenant le liquide.

La pression à ce niveau étant pc

pa . S + rho . S . h . g = pc . S

pa + rho . h . g = pc

La pression au fond du liquide est égale à la pression atmosphérique additionnée de la pression hydrostatique qui est fonction de la masse volumique, de la température et de la hauteur du liquide.

A remarquer que les pressions sont les mêmes pour le même niveau, pa = pa'

Les réactions sont les mêmes pc = pc'

Les poids sont les mêmes ( si la masse volumique et la température ne varient pas d'un point à un autre!).

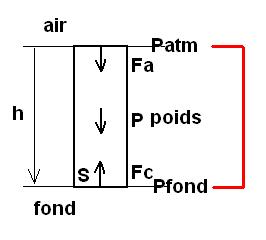
Retour sur l'élément de liquide situé entre l'air libre et le fond : on vient d'écrire que

Fa + P = Fc d'où pa + rho . h . g = pc (pa et pc sont des pressions)

ou pa tm . S - pc . S + m . g = 0 Les forces F sont égales à p . S

ou pfond. S - patm . S - m . g = 0 en inversant les signes

On va écrire que la POUSSEE D'ARCHIMEDE sur l'élément est représentée par :

Parch = ( pfond . S - patm . S ) elle est dirigée vers le haut puisque la pression au fond est supérieure à celle en surface.

On peut écrire que : Parch = m . g = ( pfond . S - patm . S ) force

Parch = rho ext . S . h . g = rho ext . V . g

La poussée d' Archimède est égale au poids du liquide extérieur à l'élément de même volume. C'est bien la définition.

Cas du ballon atmosphérique :

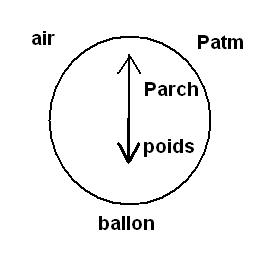
On appelle « force ascensionnelle » Fasc la différence entre Parch et le poids interne.

Fasc = Parch - poids interne du ballon

Fasc = rho ext . V . g - m . g

Fasc = rho ext . V . g - rho int . V g (équation)

Un ballon peut-il voler ? Et pourquoi ?

Il peut s'envoler si Fa est positif , Fa > 0 (1)

dans le cas contraire pas de vol possible :

si Fasc est = 0 (2)

si Fasc est < 0 (3)

Cas n° 2 : égalité dans l'équation quand les masses volumiques interne et externe sont égales.

Cas n° 3 : la charge est trop lourde, la masse volumique interne est supérieure !

Fasc = ( rho ext - rho int ). V g > 0

La force ascensionnelle sera d'autant plus forte que le volume sera grand, et que la différence des masses volumiques sera grande.

On évitera d'affirmer qu' un ballon peut voler parce qu'on lui injecte un gaz plus léger que l'air !

Quand on va utiliser des gaz comme l'hydrogène ou l'hélium, la différence est grande, et la force ascensionnelle est suffisante quelque soit la température.

Mais avec un ballon gonflé à l'air chaud, il va falloir atteindre une différence des masses volumiques assez significative pour avoir de la poussée.

Pour le cas de tous les ballons, les masses volumiques varient en fonction des températures intérieure et extérieure !

Exercice :

Supposons un ballon à air chaud gonflé avec l'air ambiant à température T1 °C.

Dessin de gauche ci-dessous.

Peut-il s'envoler ?

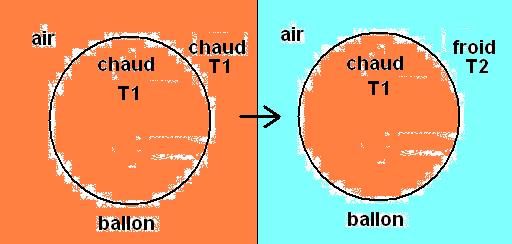
Supposons que ce ballon garde sa température T1 °C ( bon isolement !).

La température de l'air ambiant se refroidit à la température T2 °C , donc plus basse que T1 °C.

Dessin de droite ci-dessus.

Peut-il s'envoler ?

Retour sur la calcul de la Poussée d' Archimède :

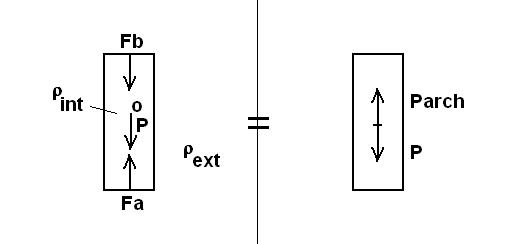
On a écrit Parch = Fa - Fb

Fasc = Parch - P

Fasc = Parch - poids interne du ballon

Fasc = rho ext . V . g - m . g

Fasc = rho ext . V . g - rho int . V g (équation)

Cas n° 2 dessin à droite, égalité et Fasc = 0

Cas n° 1 Fasc > 0

rho ext > rho int ou ce qui revient au même rho int < rho ext

La nuance est dans ce raisonnement :

ou bien on attends que la masse volumique extérieure augmente ! Voir l'exercice ballon plus haut.

ou on injecte un fluide de masse volumique interne inférieur à celui externe !

Voir comparatif des masses volumiques de quelques gaz

gaz	air		1
	ammoniac	NH3	0,597
	azote		0,967
	gaz des marais	CH4	0,558
	gaz d'éclairage		0,399
	hydrogène		0,0694
	ethylène	C2H4	0,971
	oxyde de carbone		0,967
vapeur	acide cyanhydrique		0,948
	chlorhydrate d'ammoniaque		0,93
	vapeur d'eau		0,6285
	éther		0,736

Retour sur l'élément de liquide :

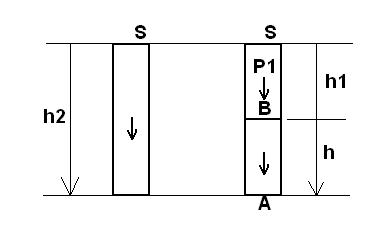
Fb = pb . S = P1 car 0 + P1 = pb . S

pb . S = rho ext . S . h1 . g

Fa = pa . S = rho ext . S . h2 . g avec 0 + P2 = pa . S

P arch = Fa - Fb = pa . S - pb . S = rho ext . S . h2 . g - rho ext . S . h1 . g

P arch = rho ext . S . g ( h2 - h1 ) = rho ext . S . g . h = rho ext . V . g

Fasc = Parch - poids interne du ballon

Fasc = rho ext . V . g - rho int . V . g

Par la suite nous reviendrons sur ces calculs en incorporant le poids des accessoires et de la charge utile que le ballon est chargé de porter à une altitude déterminée.

Écrit par Alain F6AGV pour le BHAF

documentation, bibliographie, ouvrages, livres et articles utilisés pour établir les pages :

à suivre,